Answer:
For any material if ∈ is the axial strain then the lateral strain is given by -μ∈ is the lateral strain in the object
Where,
μ is the poisson's ratio of the material
The longitudinal strain is calculated as follows

Thus the lateral strain becomes
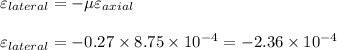
now by definition of lateral strain we have
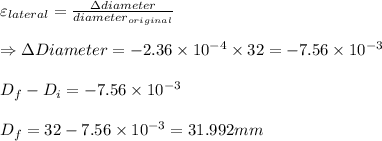
By hookes law the stress developed due to the given strain is given by

Applying values we get
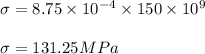
Thus the force is calculated as
