Question

A pipeline leads from one reservoir to another, which has its water surface 10 m lower. For a discharge of 1.0 m3/s, determine the losses in meters and in KW.

Answer 1

10m and 98.1 KW

Step-by-step explanation:

Data provided;

Difference between the water level of the reservoir, h = 10 m

Discharge through the pipe = 1.03 m³/s

applying the Bernoulli's theorem between the water level of the two reservoir, we have

`(P_1)/(\gamma)+(V^2_1)/(2g)+h=(P_2)/(\gamma)+(V^2_2)/(2g)+h_L`

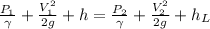
here,

P is the pressure

V is the velocity of flow

γ is the unit weight of the water = 9810 kg/m³

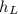`h_L` is the head loss

1 represents the water level at the reservoir at upstream and 2 representing the reservoir at downstream

now,

the pressure will be atmospheric at both the water surface and the velocity of water will be nearly zero

thus,

the above relation comes as

`h = h_L`

or

The loss is head loss of 10 m

also

P =
`\gamma Qh_L`

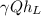
on substituting the values, we get

P = 9810 × 1 × 10 = 98100 W = 98.1 KW