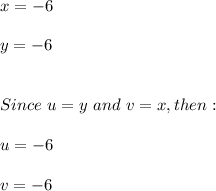Question

Solve by graphing

u=v and 6u=2v-24

Answer 1

`u=-6 \\ \\ v=-6`

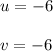
Explanation:

In this exercise, we have two equations, namely:

`u=v \ and \ 6u=2v-24`

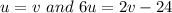
And we are asked to solve this problem by graphing. In this way, we can write a system of linear equations in two variables, but first of all, let's rewrite:

`u=y \\ \\ v=x`

Then:

`\left\{ \begin{array}{c}y=x\\6y=2x-24\end{array}\right.`

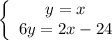
So here we have two lines.

The first one is:

`\boxed{y=x}`

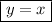
This line passes through the origin and has a slope
`m=1`

The second one is:

`6y=2x-24 \\ \\ \therefore y=(2x-24)/(6) \\ \\ \therefore \boxed{y=(1)/(3)x-4}`

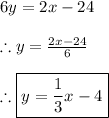
This line has a slope
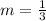`m=(1)/(3)` and cuts the y-axis at
`b=-4`

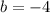
By using graph tools, we get the graph shown below, then:

`x=-6 \\ \\ y=-6 \\ \\ \\ Since \ u=y \ and \ v=x, then: \\ \\ u=-6 \\ \\ v=-6`