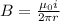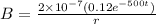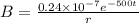Question

If an uncharged 20 uF circular plate capacitor, with R=0.10 m and separation d = 0.002 m, is hooked up in series with a 100 2 resistor to a 12 V battery. Find the magnetic field in the middle of the capacitor as a function of r and t (both inside the radius and outside).

Answer 1

inside plates

`B = (2.4 * 10^(-6))r(e^(-500 t))`

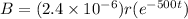
Outside plates

`B = (0.24 * 10^(-7) e^(-500 t))/(r)`

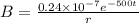
Step-by-step explanation:

As capacitor is connected with the battery and resistance then we have

`(q)/(C) + iR = V`

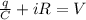
so we have

`q = CV(1 - e^(-t/RC))`

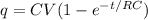
now the current in the circuit is given as

`i = (dq)/(dt)`

`i = (V)/(R)e^(-t/RC)`

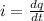
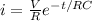
we have

`R = 100 ohm`

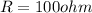
V = 12 Volts

`C = 20 \mu F`

now we have

`i = (12)/(100) e^{-t/(100* 20* 10^(-6))}`

`i = 0.12 e^(-500t)`

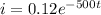
now to find the magnetic field at a distance "r" from the axis inside the plates we know

`B = (\mu_0 i r)/(2\pi R^2)`

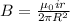
so we have

`B = (2* 10^(-7) (0.12 e^(-500 t)) r)/(0.10^2)`

`B = (2.4 * 10^(-6))r(e^(-500 t))`

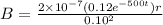
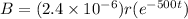
Now for outside the plates we have

`B = (\mu_0 i)/(2\pi r)`

`B = (2* 10^(-7) (0.12 e^(-500 t)))/(r)`

`B = (0.24 * 10^(-7) e^(-500 t))/(r)`