Question

A frictionless piston-cylinder device contains a saturated liquid and water vapor mixture at 110 ℃. During a constant pressure process, 546 kJ of heat is transferred to the surrounding air at 15 ℃. As a result, the vapor part inside the cylinder condenses. Determine a) the entropy change of the water and b) the generation of total entropy during this heat transfer process.

Answer 1

Step-by-step explanation:

(a) It is given that heat transferred is -546 kJ (as heat is releasing) and temperature is 110 degree celsius.

Hence, the temperature in kelvin will be as follows.

(110 + 273) K

= 383 K

As it is known that relation between entropy change and heat is as follows.

S =
`(Q)/(T)`

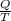
Putting the given values in the above equation as follows.

S =
`(Q)/(T)`

=
`(546 kJ)/(383 K)`

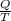
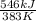
= -1.4255 kJ/K

As temperature changes from
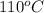`110 ^(o)C` to
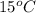`15 ^(o)C`. So, (15 + 273) K = 288 K. Hence, change in entropy will be calculated as follows.

`\Delta S = (Q)/(T)`

=
`(546 kJ)/(288 K)`

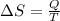
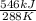
= 1.895 kJ/K

Therefore, entropy change of water will be 1.895 kJ/K.

(b) As total entropy generated will be the sum of both the entropies as follows.

Total entropy = (-1.4255 kJ/K + 1.895 kJ/K)

= 0.4695 kJ/K

Thus, total entropy during this heat transfer process is 0.4695 kJ/K.