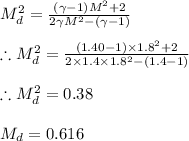Question

A normal shock wave takes place during the flow of air at a Mach number of 1.8. The static pressure and temperature of the air upstream of the shock wave are 100 kPa (abs.) and 150C. Determine the Mach number, pressure and temperature downstream of the shock.

Answer 1

The pressure upstream and downstream of a shock wave are related as

`(P_(1))/(P_(o))=(2\gamma M^(2)-(\gamma -1))/(\gamma +1)`

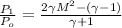
where,

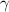`\gamma`= Specific Heat ratio of air

M = Mach number upstream

We know that
`\gamma _(air)=1.4`

Applying values we get

`(P_(1))/(100kPa)=(2* 1.4* 1.8^(2)-(1.4 -1))/(1.4 +1)\\\\(P_(1))/(100kPa)=3.61\\\\\therefore P_(1)=361.33kPa(Absloute)`

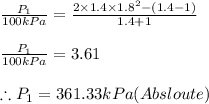
Similarly the temperature downstream is obtained by the relation

`(T_(1))/(T_(o))=([2\gamma M^(2)-(\gamma -1)][(\gamma -1)M^(2)+2])/((\gamma +1)^(2)M^(2))`

Applying values we get

`(T_(1))/(423)=([2* 1.4* 1.8^(2)-(1.4-1)][(1.4-1)1.8^(2)+2])/((1.4+1)^(2)* 1.8^(2))\\\\\therefore (T_(1))/(423)=1.53\\\\\therefore T_(1)=647.85K=374.85^(o)C`

The Mach number downstream is obtained by the relation

`M_(d)^(2)=((\gamma -1)M^(2)+2)/(2\gamma M^(2)-(\gamma -1))\\\\\therefore M_(d)^(2)=((1.40-1)* 1.8^(2)+2)/(2*1.4* 1.8^(2)-(1.4-1))\\\\\therefore M_(d)^(2)=0.38\\\\M_(d)=0.616`