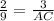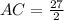Question

In AABC, point D is on AB, and point E is on BC

such that DE || AC. If DB = 2, DA = 7, and
DE = 3, what is the length of AC?
1) 8
29
3) 10.5
4) 13.5

Answer 1

`AC=(27)/(2)`

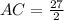
Explanation:

We are given a Triangle ABC , and DE││BC , where D and E lies on AB and BC Respectively. As DE││BC , ABC is similar to BDE. Hence the ratios of the respective sides will be equal . Hence

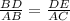`(BD)/(AB)=(DE)/(AC)` ----------(A)

Given BD=2

BA=BD+AD=2+7=9

DE=3

Putting these values in (A)

`(2)/(9)=(3)/(AC)`

`AC= (3 * 9)/(2)`

`AC=(27)/(2)`