Question

A​ true-false test consists of 11 questions. ​a) In how many ways can the test be​ completed, selecting true or false for each​ question? ​b) What is the probability that a test is randomly answered​ perfectly? ​a) In how many ways can the test be​ completed, selecting true or false for each​ question? The test can be completed in nothing ways. ​(Type a whole​ number.) ​b) What is the probability that a test is randomly answered​ perfectly? The probability is nothing. g

Answer 1

(a) 2048

(b)
`(1)/(2048)`.

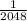Explanation:

(a)

Total number of questions = 11

Each equation has two possible answers (either true or false).

We need to find the total number of ways in which the test can be​ completed.

`\text{Total number of ways}=2* 2* 2* 2* 2* 2* 2* 2* 2* 2* 2`

`\text{Total number of ways}=2^(11)`

`\text{Total number of ways}=2048`

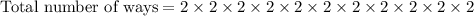
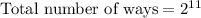
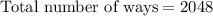
Therefore the total possible ways to complete the test is 2048.

(b)

We need to find the probability that a test is randomly answered​ perfectly.

Total Favorable outcomes = 1

Total possible ways = 2048

`Probability=\frac{\text{Total Favorable outcomes}}{\text{Total possible ways}}`

`Probability=(1)/(2048)`

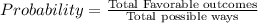
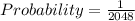
Therefore the probability that a test is randomly answered​ perfectly is
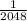`(1)/(2048)`.