Question

A cylinder shaped can needs to be constructed to hold 500 cubic centimeters of soup. The material for the sides of the can costs 0.03 cents per square centimeter. The material for the top and bottom of the can need to be thicker, and costs 0.05 cents per square centimeter. Find the dimensions for the can that will minimize production cost. Helpful information: h : height of can, r : radius of can Volume of a cylinder: V

Answer 1

r=3.628cm

h=12.093cm

Explanation:

For this problem we are going to use principles, concepts and calculations from multivariable calculus; mainly we are going to use the Lagrange multipliers method. This method is thought to help us to find a extreme value of a multivariable function 'F' given a restriction 'G'. F represents the function that we want to optimize and G is just a relation between the variables of which F depends. The Lagrange method for just one restriction is:

`\\abla F=\lambda \\abla G`

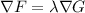
First, let's build the function that we want to optimize, that is the cost. The cost is a function that must sum the cost of the sides material and the cost of the top and bottom material. The cost of the sides material is the unitary cost (0.03) multiplied by the sides area, which is
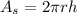`A_s=2\pi rh` for a cylinder; while the cost of the top and bottom material is the unitary cost (0.05) multiplied by the area of this faces, which is
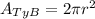`A_(TyB)=2\pi r^2` for a cylinder.

So, the cost function 'C' is:

`C=2\pi rh*0.03+2\pi r^2*0.05\\C=0.06\pi rh+0.1\pi r^2`

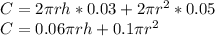
The restriction is the volume, which has to be of 500 cubic centimeters:

`V=500=\pi r^2h\\500=\pi hr^2`

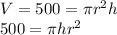
So, let's apply the Lagrange multiplier method:

`\\abla C=\lambda \\abla V\\(\partial C)/(\partial r)=0.06\pi h+0.2\pi r\\(\partial C)/(\partial h)=0.06\pi r\\(\partial V)/(\partial r)=2\pi rh\\(\partial V)/(\partial h)=\pi r^2\\(0.06\pi h+0.2\pi r,0.06\pi r)=\lambda (2\pi rh,\pi r^2)`

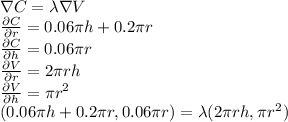
At this point we have a three variable (h,r, λ)-three equation system, which solution will be the optimum point for the cost (the minimum). Let's write the system:

`0.06\pi h+0.2\pi r=2\lambda \pi rh\\0.06\pi r=\lambda \pi r^2\\500=\pi hr^2`

(In this kind of problems always the additional equation is the restricion, in this case, V=500).

Let's divide the first and second equations by π:

`0.06h+0.2r=2\lambda rh\\0.06r=\lambda r^2\\500=\pi hr^2`

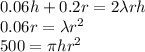
Isolate λ from the second equation:

`\lambda =(0.06)/(r)`

Isolate h from the third equation:

`h=(500)/(\pi r^2)`

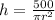
And then, replace λ and h in the first equation:

`0.06*(500)/(\pi r^2) +0.2r=2*((0.06)/(r))r(500)/(\pi r^2) \\(30)/(\pi r^2)+0.2r= (60)/(\pi r^2)`

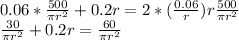
Multiply all the resultant equation by
`\pi r^(2)`:

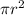`30+0.2\pi r^3=60\\0.2\pi r^3=30\\r^3=(30)/(0.2\pi ) =(150)/(\pi)\\r=\sqrt[3]{(150)/(\pi)}\approx 3.628cm`

Then, find h by the equation
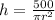`h=(500)/(\pi r^2)` founded above:

`h=(500)/(\pi r^2)\\h=(500)/(\pi (3.628)^2)=12.093cm`