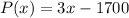Question

9. Calisto Publishing Co. sells graphic novels and comics to a large retailer for $7.50 per book. The daily cost, in dollars, for the company to print x books is

C(x) = 4.50x + 1700

Part A: What do the linear term and constant in the cost function represent?

Part B: Write a revenue function and the profit function for Calisto Publishing Co.

Answer 1

For this case we have that the cost function is given by:

`C (x) = 4.50x + 1700`

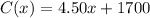
Where the linear term 4.50x represents the cost associated with the printing of "x" books.

While the constant term 1700 represents a fixed daily cost in the company. For example, the cost of maintaining the printers or the cost of transportation for the delivery of the books to the retailer.

On the other hand we have that, if retail sales are given for $ 7.50 per book, we have that the revenue function is given by:

`I (x) = 7.50x`

We can calculate the profit as:

`P (x) = I (x) -C (x)`

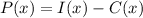
So:

`P (x) = 7.50x- (4.50x + 1700)\\P (x) = 7.50x-4.50x-1700\\P (x) = 3x-1700`

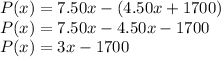
Answer:

The linear term 4.50x represents the cost associated with the printing of "x" books. The constant term 1700 represents a fixed daily cost in the company.

Profits are given by:
`P (x) = 3x-1700`