Question

Air enters an adiabatic turbine at 2.8 MPa and 400°C and expands to a lower pressure of 150 kPa. Assume an isentropic efficiency of 90% for the turbine. Determine the actual outlet temperature of the turbine.

Answer 1

The outlet temperature of turbine is 327.51 K.

Step-by-step explanation:

We know that

in adiabatic process

`PV^\gamma =C`

`(T_2)/(T_1)=\left((P_2)/(P_1)\right)^{(\gamma -1)/(\gamma )}`

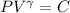
Now by putting the values

`(T_2)/(673)=\left((150)/(2800)\right)^{(1.4 -1)/(1.4 )}`

`T_2=289.39 K`

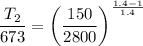
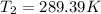
The efficiency of turbine is given as

`\eta =\frac{T_1-\acute{T_2}}{T_1-T_2}`

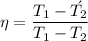
By putting the values

`0.9=\frac{673-\acute{T_2}}{673-289.39}`

`\acute{T_2}=327.51 K`

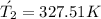
So the outlet temperature of turbine is 327.51 K.