For both ODEs, we take
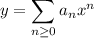
which has derivatives
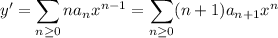
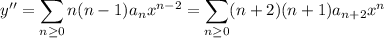
Notice that we treat
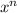 in such a way as to have
in such a way as to have
 ,
,
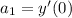 , and
, and
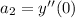
a.
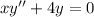
Substituting the relevant series above into the ODE gives
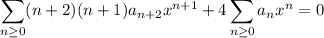
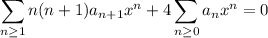
![\displaystyle\sum_(n\ge1)[n(n+1)a_(n+1)+4a_n]x^n+4a_0=0](https://img.qammunity.org/2020/formulas/mathematics/college/ypi7xrv57foztacucezcxhgk0u5paunmr2.png)
which immediately tells us
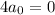 , or
, or
 , and for every other coefficient
, and for every other coefficient
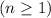 we get
we get
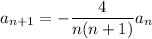
So we have
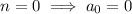

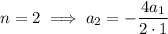
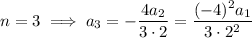
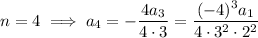
and so on, with the general pattern
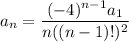
Then the first 6 non-zero terms of the solution are
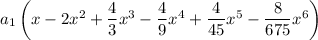
# # #
b. I'm not sure if you mean to include the third derivative, or if the last part of your post is correcting it to be the second derivative. I'll assume the latter because it's slightly simpler.
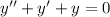
Substituting the series above into the ODE gives

![\displaystyle\sum_(n\ge0)[(n+2)(n+1)a_(n+2)+(n+1)a_(n+1)+a_n]x^n=0](https://img.qammunity.org/2020/formulas/mathematics/college/gyxqhni6w2ith2mw64qigvsflg9i0r36zr.png)
so that
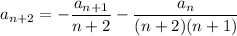
Finding a general pattern here is a bit more involved, so we'll compute the coefficients up to 6 non-zero terms:


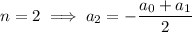
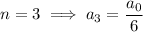
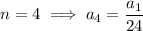
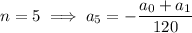
which are all non-zero as long as
 and
and
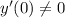 , so the first 6 non-zero terms are
, so the first 6 non-zero terms are
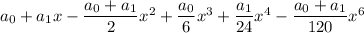
# # #
Included below are plots of the exact solutions to both ODE (in blue) along with the first 6 terms found above, with assumed initial conditions.