Question

Suppose that 112 micrograms of Vo are initially produced, after 5.00 seconds, there are 56.0 micrograms remaining. How long does it take (1) before there are only 14.0 micrograms remaining?

Answer 1

Answer: The time required will be 15 seconds.

Step-by-step explanation:

All the radioactive reactions follows first order kinetics.

The equation used to calculate half life for first order kinetics:

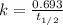`k=(0.693)/(t_(1/2))` .....(1)

Rate law expression for first order kinetics is given by the equation:

`k=(2.303)/(t)\log([A_o])/([A])` ......(2)

where,

k = rate constant

t = time taken for decay process = 5 sec

`[A_o]` = initial amount of the reactant = 112 mg

[A] = amount left after decay process = 56 mg

Putting values in above equation, we get:

`(0.693)/(t_(1/2))=(2.303)/(5)\log(112)/(56)\\\\t_(1/2)=5s`

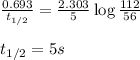
Now, calculating the rate constant from equation 1, we get:

`k=(0.693)/(5)=0.1386s^(-1)`

To calculate the time taken when 14 mg of amount remains, we use equation 2, we get:

`t=(2.303)/(5)\log (112)/(14)\\\\t=15s`

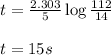
Hence, the time required will be 15 seconds.