Question

Which of the following functions I which of the following functions are one to one? Select all that apply there are 3 answers

Answer 1

The function
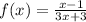`f(x)=(x-1)/(3x+3)` is one-to-one function ⇒ 1st

The function
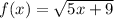`f(x)=√(5x+9)` is one-to-one function ⇒ 2nd

The function
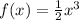`f(x)=(1)/(2)x^(3)` is one-to-one function ⇒ 4th

Explanation:

* Lets explain how to solve this problem

- One to one function is the function that has no reputation in the value

of the y-coordinates for every corresponding x-coordinates

- That means when you draw a horizontal line at any value of y, then

the horizontal line intersects the graph of the function at one point

only

- So to solve the problem look to the attached figures

# The red graph of the function
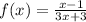`f(x)=(x-1)/(3x+3)` ⇒1st graph

- In this graph if we draw a horizontal line at any value of y it will

intersect the graph at only one point

- Take care there is a horizontal asymptote at y= 1/3, that means

there is no value of x at y = 1/3

∴ The function
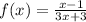`f(x)=(x-1)/(3x+3)` is one-to-one function

# The blue graph of the function
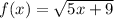`f(x)=√(5x+9)` ⇒2nd graph

- In this graph if we draw a horizontal line at any value of y it will

intersect the graph at only one point

∴ The function
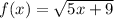`f(x)=√(5x+9)` is one-to-one function

# The green graph of the function
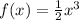`f(x)=(1)/(2)x^(3)` ⇒3rd graph

- In this graph if we draw a horizontal line at any value of y it will

intersect the graph at only one point

∴ The function
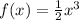`f(x)=(1)/(2)x^(3)` is one-to-one function

# The purple graph of the function
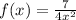`f(x)=(7)/(4x^(2))` ⇒5th graph

- In this graph if we draw a horizontal line at any value of y it will

intersect the graph at more than one point

∴ The function
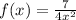`f(x)=(7)/(4x^(2))` is not one-to-one function

# The black graph of the function
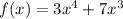`f(x)=3x^(4)+7x^(3)` ⇒4th graph

- In this graph if we draw a horizontal line at any value of y it will

intersect the graph at more than one point

∴ The function
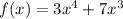`f(x)=3x^(4)+7x^(3)` is not one-to-one function

* The answers are 1st , 2nd and 4th functions