Question

A solid sphere of radius R carries a fixed, uniformly distributed charge q. Obtain an expression for the magnitude of the electric field created by the sphere at a point P outside the sphere.

Answer 1

The electric field outside the sphere will be
`(qr)/(4\pi\epsilon_(0)R^3)`.

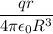Step-by-step explanation:

Given that,

Radius of solid sphere = R

Charge = q

According to figure,

Suppose r is the distance between the point P and center of sphere.

If
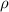`\rho` be the volume charge density,

Then, the charge will be,

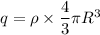`q=\rho*(4)/(3)\pi R^3`.....(I)

Consider a Gaussian surface of radius r.

We need to calculate the electric field outside the sphere

Using formula of electric field

`\oint{\vec{E}\cdot \vec{dA}}=(Q)/(\epsilon_(0))`

`E*4\pi r^2=(\rho\dotc (4)/(3)\pi r^3)/(\epsilon_(0))`

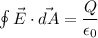
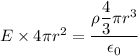
Put the value from equation (I)

`E*4\pi r^2=(qr^3)/(\epsilon_(0)R^3)`

`E=(qr)/(4\pi\epsilon_(0)R^3)`

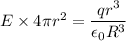
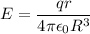
Hence, The electric field outside the sphere will be
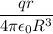`(qr)/(4\pi\epsilon_(0)R^3)`.