Answer:
a) Suppose that F is ordered in ascending order:
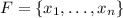 . Then, the complement of F can be written as
. Then, the complement of F can be written as
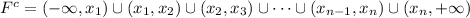
which is the union of a finite number of open intervals, then
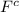 is an open set. Thus, F is a closed subset of the real numbers.
is an open set. Thus, F is a closed subset of the real numbers.
b) Take an arbitrary element of F, let us say
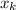 . Now, choose a real number
. Now, choose a real number
 such that
such that
](https://img.qammunity.org/2020/formulas/mathematics/college/oioupz4r36okiulav1om6bo15t4tf4jgd4.png) there are not other element of F, because
there are not other element of F, because
 is less that the minimum distance between
is less that the minimum distance between
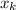 and its neighbors.
and its neighbors.
In case that
 we only consider
we only consider
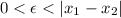 , and if
, and if
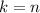 we only consider
we only consider
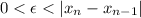 .
.
Then, all points of F are isolated.
Explanation: