Question

When a flat slab of transparent material is placed under water, the critical angle for light traveling from the slab into water is found to be 60°. What will the critical angle be if the slab is surrounded by air? Take the index of refraction for water to be 1.33. a) 40.6 b) 42.5°C) 44.2° d) 45.6°e) 47.3°

Answer 1

40.62°

Step-by-step explanation:

Case I

Light is travelling from slab (incident medium) into the water (refractive medium) , the critical angle = 60°.

The formula for the critical angle is:

`{sin\theta_(critical)}=\frac {n_r}{n_i}`

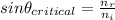
Where,

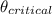`{\theta_(critical)}` is the critical angle

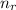`n_r` is the refractive index of the refractive medium.

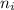`n_i` is the refractive index of the incident medium.

So,

Given that critical angle = 60°

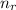`n_r` = 1.33

Applying in the formula as:

`{sin60^0}=\frac {1.33}{n_i}`

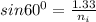
Refractive index of the slab = 1.5357

Case II

To find the critical angle when the air is the refractive medium (n=1).

So,

Applying in the formula as:

`{sin\theta_(critical)}=\frac {1}{1.5357}`

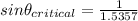
The critical angle is = sin⁻¹ 0.6511 = 40.62°