Answer:
Average power, P = 845 watts
Step-by-step explanation:
It is given that,
High power laser has a beam diameter of 1 mm, d = 1 mm
Radius, r = 0.0005 m
Electric field,
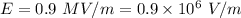
Average power of the laser is given by :
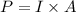
Where
I is the intensity,
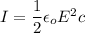
This gives,
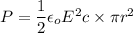
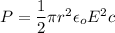
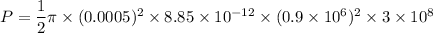
P = 844.51 watts
or
P = 845 watts
So, the average power of the laser is 845 watts. Hence, this is the required solution.