Answer:
Capacitive reactance of the capacitor is 68 ohms
Step-by-step explanation:
It is given that,
Capacitance,
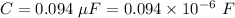
Frequency,
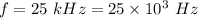
Capacitive reactance is given by :
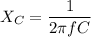
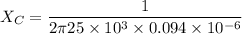
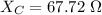
or
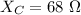
So, the capacitive reactance of the capacitor is 68 ohms. Hence, this is the required solution.