Question

A closed tank contains oxygen at 20°C at a gage pressure of 150 kPa. Determine the temperature if the oxygen is compressed isentropically to a gage pressure of 325 kPa. The atmospheric pressure is 101.3 kPa and the specific heat ratio of oxygen is 1.40. Express your answer in °C to three significant figures.

Answer 1

Step-by-step explanation:

As it is given that process is entropic which means that it is reversible adiabatic in nature.

Also, the given data is as follows.

`T_(1)` =
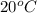`20 ^(o)C` = (20 + 273) K = 293 K

Gage pressure = 150 kPa, Atmospheric pressure = 101.3 kPa

Hence, pressure (
`P_(1)`) will be (150 kPa + 101.3 kPa) = 251.3 kPa

and, pressure (
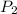`P_(2)`) will be (325 kPa + 101.3 kPa) = 426.3 kPa

Also, specific heat ratio (
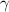`\gamma`)is given as 1.40.

Hence, relation between T and P is as follows.

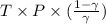`T * P * ((1 - \gamma)/(\gamma))` = constant

`T_(1)P_(1) * ((1 - \gamma)/(\gamma))` =
`T_(2)P_(2) * ((1 - \gamma)/(\gamma))`

`T_(2)` =
`T_(1) * (P_(1))/(P_(2)) * (-0.4)/(1.4)`

=
`293 K * (251.3kPa)/(426.3kPa) * (-0.4)/(1.4)`

= 340.758 K

Hence, convert this temperature into degree celsius as follows.

`(340.758 - 273) ^(o)C`

=
`67.758 ^(o)C`

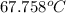
Thus, we can conclude that the temperature is
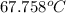`67.758 ^(o)C`.