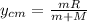Question

Starting from rest, a small block of mass m slides frictionlessly down a circular wedge of mass M and radius R which is placed on a horizontal, frictionless surface. At the moment the block leaves the wedge, it is moving a horizontally at a speed v, while the wedge slides backward at a speed V.

(a) Use appropriate conservations laws to find v and V.

(b) For the block-wedge system, how far has the center-of-mass of the system moved by the time the block slides off the wedge? In which direction did the center-of-mass move?

Answer 1

Part a)

`V = \sqrt{(2(m)/(M)gR)/(((M)/(m) + 1))}`

`v = (M)/(m)\sqrt{(2(m)/(M)gR)/(((M)/(m) + 1))}`

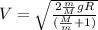
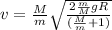
Part b)

Since on the block wedge system there is no external force in horizontal direction so the Center of mass will not move in horizontal direction but in vertical direction it will move

so displacement in Y direction is given as

`y_(cm) = (mR)/(m + M)`

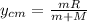
Step-by-step explanation:

PART A)

As we know that there is no external force on the system of two masses in horizontal direction

So here the two masses will have its momentum conserved in horizontal direction

So we have

`mv + MV = 0`

Also we know that here no friction force on the system so total energy will always remains conserved

So we have

`(1)/(2)mv^2 + (1)/(2)MV^2 = mgR`

now we have

`(1)/(2)m((MV)/(m))^2 + (1)/(2)MV^2 = mgR`

`(1)/(2)MV^2((M)/(m) + 1) = mgR`

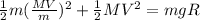
so we have

`V = \sqrt{(2(m)/(M)gR)/(((M)/(m) + 1))}`

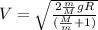
and another block has speed

`v = (M)/(m)\sqrt{(2(m)/(M)gR)/(((M)/(m) + 1))}`

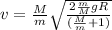
Part b)

Since on the block wedge system there is no external force in horizontal direction so the Center of mass will not move in horizontal direction but in vertical direction it will move

so displacement in Y direction is given as

`y_(cm) = (mR)/(m + M)`