Question

A sphere of radius R carries a charge density P(r) = kr, for r < R. (a) What is the field of the sphere, as a function of r? (b) What is the energy of this configuration?

Answer 1

electric field is k
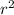`r^(2)` / ε × 4

energy is πk²
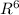`R^(6)` /48ε

Step-by-step explanation:

given data

radius = R

charge density P(r) = kr

r < R

to find out

field of the sphere and energy

solution

we know that P(r) = kr

here k is constant

we divide the sphere in many number of parts and we consider element thickness is dr so voulme will be 4πr²dr

so charge will be

dq = P ( 4πr²)dr

dq = kr ( 4πr²)dr

take integrate both side

∫dq = 4πk ∫r³ dr

q = 4πk
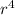`r^(4)` / 4

q = πk
`r^(4)`

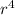
so we apply here gauss law

E×A = q / ε

electric field = πk
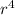`r^(4)` / ε × 4πr²

electric field = πk
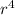`r^(4)` / ε × 4πr²

so electric field = k
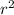`r^(2)` / ε × 4

and

in 2nd part we know

U, energy = energy density × volume

U, energy = (1/2 × ε × E²) × (4πr² )

U energy = (1/2 × ε × (kr²/4ε)²) × (4πr²)

U, energy = πk²
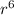`r^(6)` / 8ε

take integrate both side with 0 to U and 0 to R

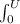`\int_(0)^(U)`dU = πk²/8ε
`\int_(0)^(R)`
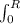
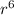`r^(6)` dr

U, energy = πk²/8ε ×
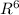`R^(6)` /6

so energy = πk²
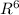`R^(6)` /48ε