Question

Sari is teaching her best friend how to factor trinomials with a leading coefficient greater than 1. She starts with the trinomial

2x^2+5x+3


Show/Describe all of the steps for finding the factorization of the trinomial. Be sure to include the final factorization in your description.

Answer 1

See explanation

`2x^2+5x+3=(x+1)(2x+3)`

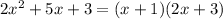
Explanation:

1. Make sure that the trinomial is written in the correct order - the trinomial must be written in descending order from highest power to lowest power. In you case, the trinomial must be written as

`2x^2+5x+3`

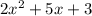
2. Decide if the three terms have anything in common, called the greatest common factor or GCF. If so, factor out the GCF. Do not forget to include the GCF as part of your final answer.

In your case, coefficients 2, 5 and 3 do not have common factors, so go to the next step.

3. Multiply the leading coefficient and the constant, that is multiply the first and last numbers together:

`2\cdot 3=6`

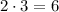
4. List all of the factors from step 3 and decide which combination of numbers will combine to get the number next to x:

`6=1\cdot 6\\ \\ \bf{6=2\cdot 3}`

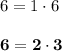
5. After choosing the correct pair of numbers, you must give each number a sign so that when they are combined they will equal the number next to x and also multiply to equal the number found in Step 3:

`2+3=5`

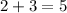
6. Rewrite the original problem with four terms by splitting the middle term into the two numbers chosen in step 5:

`2x^2+5x+3=2x^2+2x+3x+3`

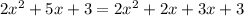
7. Now that the problem is written with four terms, you can factor by grouping:

`2x^2 +2x+3x+3=(2x^2+2x)+(3x+3)=2x(x+1)+3(x+1)=(x+1)(2x+3)`