Question

A saturated solution prepared at 70∘C contains 32.0 g CuSO4 per 100.0 g solution. A 350 −g sample of this solution is then cooled to 0∘C and CuSO4⋅5H2O crystallizes out. If the concentration of a saturated solution at 0∘C is 12.5 gCuSO4/100 g soln, what mass of CuSO4⋅5H2O would be obtained? [Hint: Note that the solution composition is stated in terms of CuSO4 and that the solid that crystallizes is the hydrate CuSO4⋅5H2O.] Express your answer using two significant figures.

Answer 1

`1.6x10^(2)gCuSO_4\ ^.5H_2O`

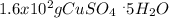
Step-by-step explanation:

Hello,

In this case, the mass of copper (II) sulfate that are available for the 350-g sample is:

`m_(CuSO_4)=0.32(gCuSO_4)/(gSample) *350gSample=112gCuSO_4`

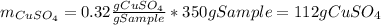
And the mass of water:

`m_(H_2O)=350g-112g=238gH_2O`

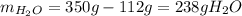
Now, the dissolved copper (II) sulfate at 0°C is:

`350gSample*0.125(gCuSO_4)/(gSample) =43.75gCuSO_4`

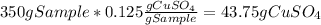
Therefore, the undissolved copper (II) sulfate is:

`m_(CuSO_4)^(undissolved)=112-43.75=68.25gCuSO_4`

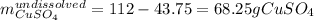
In addition, 238 g of water are equivalent to 13.5 moles of water, nevertheless, as a pentahydrate is obtained, 5 moles of water correspond to:

`m_(H_2O)^(crystalized)=(5mol*238g)/(13.2mol)=90.152g H_2O`

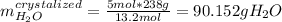
Therefore, the mass of copper (II) sulfate pentahydrate turns out:

`m_(CuSO_4\ ^.5H_2O)=68.25g+90.152g=1.6x10^(2)gCuSO_4\ ^.5H_2O`

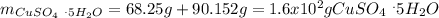
Best regards.

Answer 2

Step-by-step explanation:

gram of Copper sulphate in 350 g solution is 32 x 3.5 = 112

in term of mol = 112 / 159.5 = 0.7022

after crystallisation, gm of copper sulphate in the solution

= 43.75

in term of mole

43.75/159.5 = 0.2743

mole that got precipitated in hydrated form = 0.7022 - 0.2743 =0.4279

in terms of gm of hydrated copper sulphate = .4279 x mol weight of hydrated copper sulphate = .4279 x 249.5 = 106.76 g .