Question

4. [5 pts] Describe how and why the formula for permutations differs from the formula for combinations.

Answer 1

They are different because of the order in the permutation matters. In combination, the order doesn't matter. In other words in a permutation 123 and 132 are different but in a combination are the same group (they have the same digits 1,2, and 3).

Explanation:

The formula of the permutation is
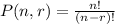`P(n,r)=(n!)/((n-r)!)`, when you are performing a permutation you pick r objects from a total of n, for the first pick you can choose from n, but for the second you have n-1, and this continues to your pick number r in which you will choose from n-r+1, and the total of permutation is the multiplicación of this number of choices for each pick, like this:

`n(n-1)(n-2)...(n-r+1)`

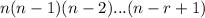
If
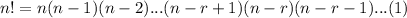`n!=n(n-1)(n-2)...(n-r+1)(n-r)(n-r-1)...(1)` and
`(n-r)!=(n-r)(n-r-1)(n-r-2)...(1)`

`(n!)/((n-r)!)=(n(n-1)(n-2)...(n-r+1)(n-r)(n-r-1)...(1))/((n-r)(n-r-1)(n-r-2)...(1))`

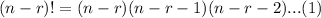
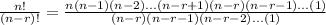
The factor equals above and under cancel each other.

`(n!)/((n-r)!)=(n(n-1)(n-2)...(n-r+1)(n-r)(n-r-1)...(1))/((n-r)(n-r-1)(n-r-2)...(1))\\(n!)/((n-r)!)=n(n-1)(n-2)...(n-r+1)`

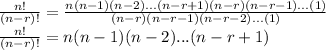
In combination, the order of the element isn't important, so from the total of permutation you have to eliminate the ones with the same objects with different order and counting just once each group, when choosing r objects the total of permutation for a single group of r objects is:
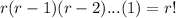`r(r-1)(r-2)...(1)=r!`. If you divide the total of permutations of n taking r by r! you get the combinations (where the order is not important). The formula of the combination is
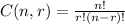`C(n,r)=(n!)/(r!(n-r)!)`.