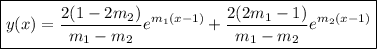Question

(3) x^2y" = 2xy - (y), y(1) = 4, 7(1) = 2 ololutions to the homogene

Answer 1

My best guess at interpreting this question is that you need to solve

`x^2y''=2xy'-y`

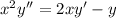
which seems like a reasonable interpretation as this ODE is of a well-known type (Cauchy-Euler). And it looks like you're given two initial conditions,
`y(1)=4` and
`y'(1)=2`.

`x^2y''-2xy'+y=0`

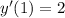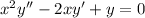
Substitute
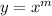`y=x^m`, so that
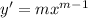`y'=mx^(m-1)` and
`y''=m(m-1)x^(m-2)`. Then plugging these into the ODE gives

`m(m-1)x^m-2mx^m+x^m=0`

`m(m-1)-2m+1=0`

`m^2-3m+1=0`

`\implies m_1=\frac{3+\sqrt5}2,m_2=\frac{3-\sqrt5}2`

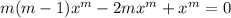
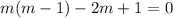
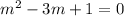
So the homogeneous ODE has general solution

`y=C_1e^(m_1x)+C_2e^(m_2x)`

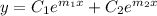
This solution has derivative

`y'=m_1C_1e^(m_1x)+m_2C_2e^(m_2x)`

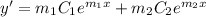
From the initial conditions, we get

`4=C_1e^(m_1)+C_2e^(m_2)`

`2=m_1C_1e^(m_1)+m_2C_2e^(m_2)`

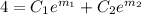
Solving this system gives

`C_1=(2e^(-m_1)(1-2m_2))/(m_1-m_2),C_2=(2e^(-m_2)(2m_1-1))/(m_1-m_2)`

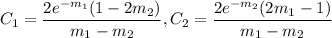
thus giving the particular solution,

`\boxed{y(x)=(2(1-2m_2))/(m_1-m_2)e^(m_1(x-1))+(2(2m_1-1))/(m_1-m_2)e^(m_2(x-1))}`