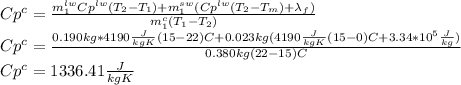Question

A 380 g metal container, insulated on the outside, holds 190 g of water in thermal equilibrium at 22°C. A 23 g ice cube, at the melting point, is dropped into the water, and when thermal equilibrium is reached the temperature is 15°C. Assume there is no heat exchange with the surroundings. For water, the specific heat capacity is 4190 J/kg ∙ K and the heat of fusion is 3.34 × 105 J/kg. The specific heat capacity for the metal is closest to:

3440 J/kg ∙ K
2340 J/kg ∙ K
1340 J/kg ∙ K
840 J/kg ∙ K
2840 J/kg ∙ K

Answer 1

C) 1340 J/kg K

Step-by-step explanation:

This problem can be solved by applying an energy balance for the whole process. The energy is initially in the container (superscript C), the liquid water (superscript lw) and the ice or solid water (superscript sw), where the liquid water and the ice are still unmixed:

`U^c+U^(lw)+U^(sw)`

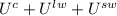
The energy is in the final state in the container and a liquid water mass which is greater than the first one.

`U^c+U^(lw)`

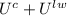
Without any heat transfer, the initial and the final energy must be the same, so:

`U_1=U_2`

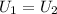
The initial and final states are denoted with 1 and 2 subscripts respectively.

`U_1^(c)+U_1^(lw)+U_1^(sw)=U_2^(c)+U_2^(lw)`

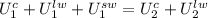
Reorganizing, and expressing the internal energies as a product of the mass by the specific internal energy:

`U_1^(c)-U_2^(c)=U_2^(lw)-U_1^(lw)-U_1^(sw)\\m_1^(c)(u_1^(c)-u_2^(c))=m_2^(lw)u_2^(lw)-m_1^(lw)u_1^(lw)-m_1^(sw)u_1^(sw)`

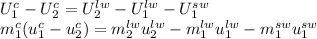
Then, note that the mass of the liquid water in the final state is the sum of the initial water mass and the mass of the ice added:

`m_2^(lw)=m_1^(lw)+m_1^(sw)`.

We can replace this equation in the energy balance we had:

`m_1^(c)(u_1^(c)-u_2^(c))=(m_1^(lw)+m_1^(sw))u_2^(lw)-m_1^(lw)u_1^(lw)-m_1^(sw)u_1^(sw)\\m_1^(c)(u_1^(c)-u_2^(c))=m_1^(lw)u_2^(lw)+m_1^(sw)u_2^(lw)-m_1^(lw)u_1^(lw)-m_1^(sw)u_1^(sw)\\m_1^(c)(u_1^(c)-u_2^(c))=m_1^(lw)(u_2^(lw)-u_1^(lw))+m_1^(sw)(u_2^(lw)-u_1^(sw))`

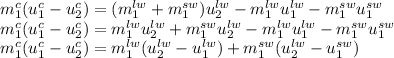
The specific internal energy change for a temperature change without phase change can be calculated by the specific heat capacity, as the specific heat at constant volume 'Cv' is so close to the specific heat at constant pressure 'Cp' for solids and liquids. So, the specific internal energy changes
`u_1^(c)-u_2^(c)` and
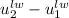`u_2^(lw)-u_1^(lw)` can be written as
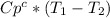`Cp^c*(T_1-T_2)` and
`Cp^(lw)(T_2-T_1)` respectively. So, our energy balance comes up:

`m_1^(c)Cp^c*(T_1-T_2)=m_1^(lw)Cp^(lw)(T_2-T_1)+m_1^(sw)(u_2^(lw)-u_1^(sw))`

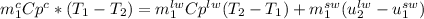
Now, the internal specific energy change
`u_2^(lw)-u_1^(sw)` is an energy change which involves a phase change, so it can't be calculated as the others. However, this internal specific energy change can be calculated by steps, first melting the ice and then heating the water. When melting the ice the associated energy is the heat of fusion:
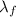`\lambda _f` and when heating the liquid water the associated energy is (as it does not involve a phase change)
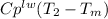`Cp^(lw)(T_2-T_m)` where
`T_m` is the melting temperature. Bear in mind that for the calculation of
`u_2^(lw)-u_1^(sw)` we are assuming that we melt the ice obtaining liquid water at 0 ºC (the melting temperature) and then heat it to the final temperature (
`T_2`). Then, the internal specific energy change
`u_2^(lw)-u_1^(sw)` is:

`u_2^(lw)-u_1^(sw)=Cp^(lw)(T_2-T_m)+\lambda _f`

At this point, our energy balance is:

`m_1^(c)Cp^c*(T_1-T_2)=m_1^(lw)Cp^(lw)(T_2-T_1)+m_1^(sw)(Cp^(lw)(T_2-T_m)+\lambda _f)`

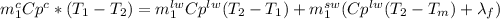
And our only unknown quantity is
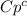`Cp^c`, so let's find it:

`Cp^c=(m_1^(lw)Cp^(lw)(T_2-T_1)+m_1^(sw)(Cp^(lw)(T_2-T_m)+\lambda _f))/(m_1^(c)(T_1-T_2)) \\Cp^c=(0.190kg*4190(J)/(kgK) (15-22)C+0.023kg(4190(J)/(kgK)(15-0)C+3.34*10^5(J)/(kg)))/(0.380kg(22-15)C)\\Cp^c=1336.41(J)/(kgK)`