Question

An Object is located 16 cm in front of a converging lens with focal length 12 cm. To the right of the converging lens, separated by a distance of 20 cm, is a diverging lens of focal length -10cm. Find the location of the final image.

Answer 1

image is located at 22.5cm to the left of diverging lens.

Step-by-step explanation:

In this question we have given,

object distance from converging lens,u=-16cm

focal length of converging lens,
`f_(c)=12cm`

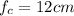
focal length of diverging lens,
`f_(d)=-10cm`

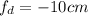
distance between converging and diverging lens=20cm

we have to find location of final image,v=?

Here we will first find the location of image formed by converging lens

we know that u, v and
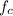`f_(c)` are related by following formula

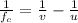`(1)/(f_(c)) =(1)/(v)- (1)/(u)`.............(1)

put values of
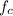`f_(c)` and u in equation (1)

we got,

`(1)/(12) =(1)/(v)- (1)/(-16)`

`(1)/(12)-(1)/(16) =(1)/(v)`

`(16-12)/(16* 12) =(1)/(v)`

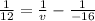
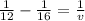
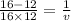
or

`v=(16* 12)/(16-12)\\ v=48cm`

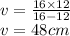
The image is located 48 cm to the right of the converging lens. This image is real and inverted.

This image will object for the diverging lens which is now located (48-20=18) cm at the right hand side of diverging lens

it means,

u=18cm

we know that u, v and
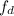`f_(d)` are related by following formula

`(1)/(f_(d)) =(1)/(v)- (1)/(u)`.............(2)

put values of
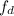`f_(d)` and u in equation (2)

`(1)/(-10) =(1)/(v)- (1)/(18)`

`(1)/(-10)+(1)/(18) =(1)/(v)`

`(-18+10)/(10* 18) =(1)/(v)`

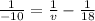
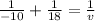
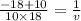
or

`v=(10* 18)/(10-18)\\ v=-22.5cm`

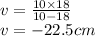
It means image is located at 22.5cm to the left of diverging lens.