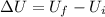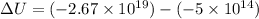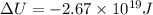Question

A stellar core of mass 3.0 x 10^30 kg and radius 4.0 x 10^8 m collapses, with no loss of mass, to become a neutron star with radius 7.5 x 10^3 m. What is the change in gravitational potential energy of 1.0 × 10^3 kg of material that was initially at the surface of the stellar core and that ends up at the surface of the neutron star?

Answer 1

`\Delta U = -2.67 * 10^(19) J`

Step-by-step explanation:

Initial gravitational potential energy of the system

`U_i = -(GMm)/(R)`

`U_i = - ((6.67 * 10^(-11))(3.0 * 10^(30))(1.0 * 10^3))/(4.0* 10^8)`

`U_i = -5.0 * 10^(14) J`

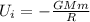
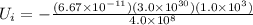
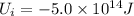
Now when star becomes a neutron star then it will convert into a denser star with no loss in mass

So it is given as

`U_f = -(GMm)/(r)`

`U_f = - ((6.67 * 10^(-11))(3.0 * 10^(30))(1.0 * 10^3))/(7.5 * 10^3)`

`U_f = -2.67 * 10^(19) J`

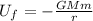
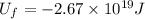
Change in the potential energy of the system is given as

`\Delta U = U_f - U_i`

`\Delta U = (-2.67 * 10^(19)) - (-5 * 10^(14))`

`\Delta U = -2.67 * 10^(19) J`