Question

A 10-mm diameter smooth pipe has a laminar flow of water with Darcy friction factor (f) equal to 0.04. What is the volume flow rate in the pipe?

Answer 1

Q=0.00274 Lt/s

Step-by-step explanation:

Given that

Darcy friction factor f=0.04

Diameter of pipe d=10 mm

We know that for laminar flow

`Re=(16)/(f)`

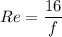
Where Re is the Reynolds number and f is the friction factor.

Now by putting the values

`Re=(16)/(0.04)`

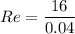
Re=400

We know that
`Re=(\rho Vd)/(\mu )`

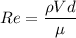
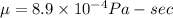`\mu =8.9* 10^(-4) Pa-sec` for water

`400=(1000 * 0.01V)/(8.9* 10^(-4))`

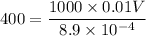
V=0.035 m/s

So volume flow rate Q=AV

`Q=(\pi)/(4)* 0.01^2* 0.035`

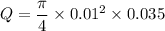
Q=0.00274 Lt/s