Question

Consider the following reaction where Kc = 77.5 at 600 K:CO(g) + Cl2(g) COCl2(g)A reaction mixture was found to contain 2.09×10-2 moles of CO(g), 4.17×10-2 moles of Cl2(g) and 0.103 moles of COCl2(g), in a 1.00 Liter container.Indicate True (T) or False (F) for each of the following:1. In order to reach equilibrium COCl2(g) must be consumed.2. In order to reach equilibrium Kc must decrease.3. In order to reach equilibrium CO must be produced.4. Qc is greater than Kc.5. The reaction is at equilibrium. No further reaction will occur.

Answer 1

Answer for the given statements: (1) T , (2) F , (3) T , (4) T , (5) F

Step-by-step explanation:

At the given interval, concentration of CO =
`(2.09* 10^(-2))/(1)M=2.09* 10^(-2)M`

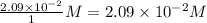
Concentration of Cl_{2} =
`(4.17* 10^(-2))/(1)M=4.17* 10^(-2)M`

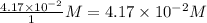
Concentration of COCl_{2} = \frac{0.103}{1}M=0.103M

Reaction quotient,
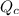`Q_(c)` , for this reaction =
`([COCl_(2)])/([CO][Cl_(2)])`

species inside third bracket represents concentrations at the given interval.

So,
`Q_(c)=((0.103))/((4.17* 10^(-2))* (2.09* 10^(-2)))=118`

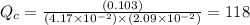
So, the reaction is not at equilibrium.

As Q_{c}> K_{c} therefore reaction must run in reverse direction to reduce Q_{c} and make it equal to K_{c}. That means
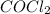`COCl_(2)`(g) must be consumed and CO must be produced.