Question

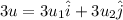
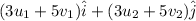
Given vectors u and v, find (a) 3u (b) 3u +5v (c) v-5u. 3(Type your answer in terms of i and j)

Answer 1

a.
`3u=3u_1\hat{i}+3u_2\hat{j}`

b.3u+5v=
`(3u_1+5v_1)\hat{i}+(3u_2+5v_2)\hat{j}`

c.v-5u=
`(v_1-5u_1)\hat{i}+(v_2-5u_2)\hat{j}`

Explanation:

Let given vector u and v are

`u=<u_1,u_2>`

`v=<v_1,v_2>`

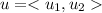
a.We have to find 3u

We are multiplying u by 3 then we get

`3u=<3u_1,3u_2>`

`3u=3u_1\hat{i}+3u_2\hat{j}`

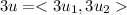
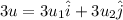
b.We have ton find the value of 3u+5v

We are multiplying u by 3

3u=<3u_1,3u_2>

We are multiplying v by 5 then we get

`5v=<5v_1,5v_2>`

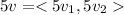
Adding 3u with 5v then we get

`3u+5v=<3u_1+5v_1,3u_2+5v_2>`

`3u+5v=(3u_1+5v_1)\hat{i}+(3u_2+5v_2)\hat{j}`

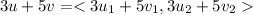
c.We have to find the value of v-5u

We are multiplying u by 5 then we get

`5u=<5u_1,5u_2>`

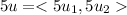
Now,v-5u=
`(v_1,v_2)-5(u_1,u_2)`

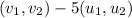
v-5u=
`(v_1-5u_1)\hat{i}+(v_2-5u_2)\hat{j}`