Step-by-step explanation:
It is given that,
Magnetic field, B = 0.5 T
Speed of the proton, v = 60 km/s = 60000 m/s
The helical path followed by the proton shown has a pitch of 5.0 mm, p = 0.005 m
We need to find the angle between the magnetic field and the velocity of the proton. The pitch of the helix is the product of parallel component of velocity and time period. Mathematically, it is given by :

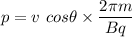
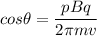
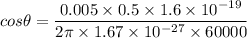

So, the angle between the magnetic field and the velocity of the proton is 50.58 degrees. Hence, this is the required solution.