Which shows the correct solution of the equation(1)/(2) a + (2)/(3) b = 50, when b= 30?

Question

Which shows the correct solution of the equation
`(1)/(2) a + (2)/(3) b = 50`, when b= 30?

Answer 1

Answer:
`a=60`

Explanation:

You have the following equation:

`(1)/(2) a + (2)/(3) b = 50`

In order to find the solution of the given equation when
`b=30`, you need to substitute this value of "b" into the equation and then you must solve for "a".

Applying this procedure, you get that the solution of the equation when
`b=30` is:

`(1)/(2) a + (2)/(3) b = 50\\\\(1)/(2) a + (2)/(3)(30) = 50\\\\(1)/(2) a + (60)/(3) = 50\\\\(3a+120)/(6)=50\\\\3a=(6)(50)-120\\\\a=(180)/(3)\\\\a=60`

Answer 2

{a:a=60}

Explanation:

The given equation is

`(1)/(2)a+(2)/(3)b=50`

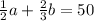
We first multiply through by the Least Common Multiple of 2 and 3, and simplify.

`\implies6*(1)/(2)a+6 *(2)/(3)b=50* 6`

`\implies3a+2(2b)=300`

`\implies3a+4b=300`

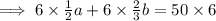
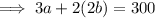
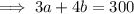
We then make a the subject,so we subtract 4b from both sides of the equation to get

`3a=300-4b`

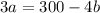
We then divide through by 3

`\implies(3a)/(3)=(300)/(3)-(4b)/(3)`

`\implies a=100-(4b)/(3)`

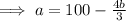
We substitute b=30 into the simplified equation to get

`a=100-(4(30))/(3)`

`\implies a=100- (120)/(3)`

`\implies a={100-40}`

`\implies a=60`

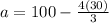
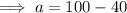
Hence the correct solution of the equation is {a:a=60}