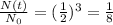Question

The half-life of a certain element is 100 days. How many half-lives will it be before only one-eighth of this element remains?

2
3
8
12.5

Answer 1

Option (2) 3

Step-by-step explanation:

Answer 2

3

Step-by-step explanation:

The half-life is the time it takes for the amount of radioactive isotope to halve. Therefore, we have:

- After 1 half-life, only 1/2 of the element will be left

- After 2 half-lives, only 1/4 of the element will be left

- After 3 half-lives, only 1/8 of the element will be left

So, it will take 3 half-lives for the element to become 1/8 of its original amount.

Mathematically, this can be also verified by using the equation

`(N(t))/(N_0)=((1)/(2))^(t)/(\tau_(1/2))`

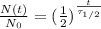
where

N(t) is the amount of the element left at time t

N0 is the initial amount of the element

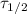`\tau_(1/2)` is the half-life

Substituting
`t=3\tau_(1/2)` (3 half-lives), we find

`(N(t))/(N_0)=((1)/(2))^3=(1)/(8)`