Question

Derive an expression for the de Broglie wavelength of a thermal neutron and calculate its value at the temperature T = 290 K. The kinetic energy of the neutron at a given temperature T is approximately 3kT/2 where k = 1.38 x 10-23 J/K is the Boltzmann constant. The neutron mass is mn 1.67 x 10-27 kg and the Planck constant h = 6.626 x 10-34 Js.

Answer 1

1.479 A

Step-by-step explanation:

Expression for de Broglie wave length

λ =
`(h)/(\left ( 2mKE \right )^(.5))`

Where m is mass of neutron ,h is plank constant and KE is kinetic energy of

proton.

Kinetic Energy ( KE) = 3 / 2 kT

=1.5 X 1.38 X 10⁻²³ X 290 = 600.3 X 10⁻²³ J

`√(2mKE)` =
`\sqrt{2*1.67*10^(-27)*600.3*10^(-23)}`

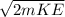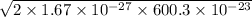
44.777 x 10⁻²⁵

λ =
`(6.626*10^(-34))/(44.777*10^(-25))`

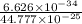
=1.479 A.