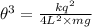Question

Two particles each of mass m and charge q are suspended by strings of length / from a common point. Find the angle e that each string makes with the vertical. (Assume 0 is small so sin 0~tan 0~0.) [Hint: consider the vertical and horizontal components of the forces acting on each particle.]

Answer 1

`\theta =\left ((kq^(2))/(4L^(2)* mg)  \right )^{(1)/(3)}`

Step-by-step explanation:

Let the length of the string is L.

Let T be the tension in the string.

Resolve the components of T.

As the charge q is in equilibrium.

T Sinθ = Fe ..... (1)

T Cosθ = mg .......(2)

Divide equation (1) by equation (2), we get

tan θ = Fe / mg

`tan\theta =((kq^(2))/(AB^(2)))/(mg)`

`tan\theta =\frac{(kq^(2))/(4L^(2)Sin^(\theta ))}}{mg}`

`tan\theta =(kq^(2))/(4L^(2)Sin^(2)\theta * mg)`

`tan\theta* Sin^(2)\theta =(kq^(2))/(4L^(2)* mg)`

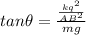
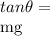
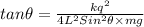
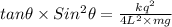
As θ is very small, so tanθ and Sinθ is equal to θ.

`\theta ^(3) =(kq^(2))/(4L^(2)* mg)`

`\theta =\left ((kq^(2))/(4L^(2)* mg)  \right )^{(1)/(3)}`