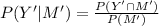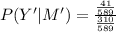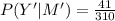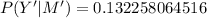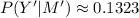Answer:
(a)
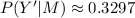
(b)
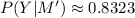
(c)
Explanation:
Given table is
Yes No Don't Know Total
Men 162 92 25 279
Women 258 41 11 310
Total 420 133 36 589
According the the conditional probability, if A and B are two event then
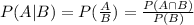
We need to find the following probabilities.
Let Y is the event "saying yes," and M is the event "being a man."
(a)
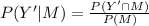
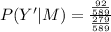
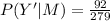
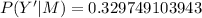
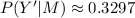
(b)
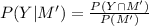
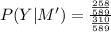
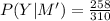
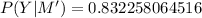
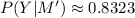
(c)