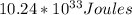Question

Find the kinetic energy ofan electron that moves at half the speed of light to four significant digits.

Answer 1

Ke=electron kinetic energy=
`10.24*10^(33) J`

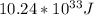
Step-by-step explanation:

The electron has a mass of
`9.1*10^(-31) kg`

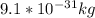
The speed of light in a vacuum is a universal constant with the value 299 792 458 m / s (186 282,397 miles / s), although it is usually close to
`3*10^(8) (m)/(s)`

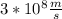
Kinetic energy (K) is the energy associated with bodies that are in motion, depends on the mass and speed of the body and is calculated using the formula:

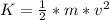`K=(1)/(2) *m*v^(2)` Equation(1)

K=kinetic energy (J)

m =mass of the body (kg)

v= speed of the body
`((m)/(s) )`

for this problem We replace in the equation (1)

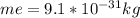`me=9.1*10^(-31) kg` = electron mass

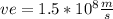`ve=1.5*10^(8) (m)/(s)`=Half the speed of light

=electron speed

We replace in the equation (1) :

`Ke=(1)/(2)*me*ve^(2)`

`Ke=(1)/(2) *9.1*10^(-31) *(1.5*10^(8) )^(2)`

`Ke=4.55*10^(-31) *(1.5)^(2) *(10^(8) )^(2)`

`Ke=10.24*10^(33) J`

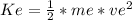
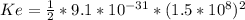
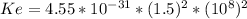
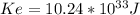
The energy kinetic of the electron is
`10.24*10^(33) Joules`