Question

Suppose a simple random sample of size nequals45 is obtained from a population with muequals64 and sigmaequals14. ​(a) What must be true regarding the distribution of the population in order to use the normal model to compute probabilities regarding the sample​ mean? Assuming the normal model can be​ used, describe the sampling distribution x overbar. ​(b) Assuming the normal model can be​ used, determine ​P(x overbarless than68.1​). ​(c) Assuming the normal model can be​ used, determine ​P(x overbargreater than or equals66.3​).

Answer 1

Explanation:

Given that sample size = n=45

mu = 64 and sigma =14

a) Sample mean will follow a normal distribution irrespective of the original distributions provided

i) samples are randomly drawn

ii) samples represent the population

iii) Sample size is sufficiently large

b) Here we have sample std dev=
`(\sigma)/(√(n) ) \\=(14)/(√(45) ) \\=2.09`

`P(X bar>68.1) = P(Z>(68.1-64)/(2.09) \\=P(Z>1.96)\\=0.25`

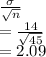
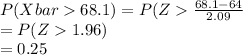
c)
`P(X bar>66.3) = P(Z>(66.3-64)/(2.09) \\=P(Z>1.10)\\=0.136`