Answer:
3867.2 m/s
4.25 x 10⁻⁵ eV
Step-by-step explanation:
Δx = uncertainty in electron's position = 15 nm = 15 x 10⁻⁹ m
Δv = uncertainty in the velocity of electron = ?
m = mass of electron = 9.1 x 10⁻³¹ kg
Using heisenberg uncertainty principle
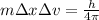
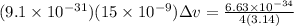
Δv = 3867.2 m/s
v = minimum speed of electron = 3867.2 m/s
Minimum kinetic energy is given as
KE = (0.5) m v²
KE = (0.5) (9.1 x 10⁻³¹) (3867.2)²
KE = 6.8 x 10⁻²⁴ J
KE =
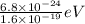
KE = 4.25 x 10⁻⁵ eV