Answer:
Option B. 1,100 Earth diameters
Solution:
Angular position of steroid,
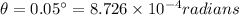 (given)
(given)
To calculate the distance of asteroid, we use parallax method given as:
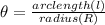 (1)
(1)
where,
From the relation:
l =

we get:
distance(d) or R =
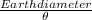
distance(d) or R =
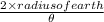
d =
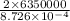
distance, d =

Comparing it with Earth's diameter:
d =
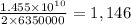
Since, the value is close to 1,100 Earth diameters, therefore, option B is the right answer.