Question

Maria has a square brick patio. She wants to reduce the width by 5 feet and increase the length by 5 feet.

Answer 1

option A

Explanation:

we have from statement:

x=length of one side of the square patio

area of original patio= x*x=x^2 = 12*12

x=12

She wants to reduce the width by 5 feet : x-5

She wants increase the length by 5 feet: x+5

area= length*width

area of the new patio= (x+5)*(x-5)

area of the new patio= (12+5)*(12-5)

area of the new patio= (17)*(7)

area of the new patio= 119 square feet

Answer 2

Answer: The correct option is

(A) lw = (x+5)(l-5); 119 square feet.

Step-by-step explanation: Given that x represents the length of one side of the square patio.

We are to write the expressions for the length and width of the new patio. Also, to find the area of the new patio if the original patio measures 12 feet by 12 feet.

From the figure, we note that

the length of the new patio is 5 feet more than x and the width of the new patio is 5 feet less than x.

That is, l = x+5 and w = x-5.

So, the expression for the area of the new patio is

`A=lw=(x+5)(x-5).`

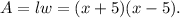
If x = 12 feet, then the area of the new patio is

`A=(12+5)(12-5)=17*7=119.`

Thus, the required expression for the new patio is
`lw=(x+5)(x-5)`. And, the area of the new patio if the original patio is 12 feet by 12 feet is 119 square feet.

Option (A) is CORRECT.