Question

A truck using a rope to tow a 2230-kg car accelerates from rest to 13.0 m/s in a time of 15.0s. How strong must the rope be? μk = 0.373

Answer 1

The rope must have a force of 10084,21 N

Step-by-step explanation

Acceleration calculation

The car acceleration is equal to the acceleration of the truck

ac: car acceleration
`(m)/(s^(2) )`

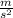
at: truck acceleration
`(m)/(s^(2) )`)

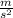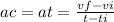`ac = at= (vf-vi)/(t-ti)` equation(1)

Known information:

vi = Initial speed = 0, ti = initial time = 0

vf = Final speed = 13
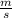`(m)/(s)`, t = final time =5 s

We replaced the known information in the equation(1):

`ac = at = (13-0)/(15-0)`

`ac=ac=(13)/(15)  (m)/(s)`

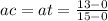
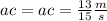
Dynamic analysis

The forces acting on the car are the following:

Wc: Car weight

N: normal force, road force on the car

Ff: Friction force

T: Force of tension

Car weight calculation:

`Wc=mc*g`

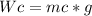
mc = Car mass = 2230kg

g = Gravity acceleration=9.8
`(m)/(s^(2) )`

`Wc= 2230*9.8`

`Wc=21854 N`

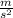
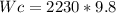
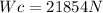
Normal force calculation:

Newton's first law

`sum Fy= 0`

`N-W=0`

`N=W`

`N=21854 N`

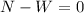
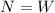
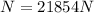
Friction force calculation (Ff):

We have the formula to calculate the friction force:

Ff = μk * N Equation (3)

μk kinetic coefficient of friction

We know that μk = 0.373and N= 21854N ,then:

`Ff=0.373*21854`

`Ff=8151.54 N`

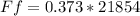
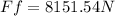
Calculation of the tension force in the rope (T):

Newton's Second law

`sum Fx= mc*ac`

`T-Ff=mc*ac`

`T=2230((13)/(15)) + 8151.54`

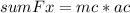
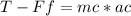
T=10084,21 N

Answer: The rope must have a force of 10084,21 N