Answer:
Diameter, d = 4237.14 meters
Step-by-step explanation:
It is given that,
On earth you can jump straight up a distance of 36 cm, h = 36 cm = 0.36 m
Asteroids are made of material with mass density,
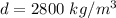
Escape velocity is given by :

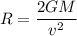
Where
G is the universal gravitational constant
M is the mass
Density,
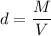
Density,

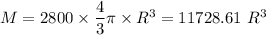 ..............(2)
..............(2)
Now using conservation of energy as :
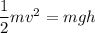
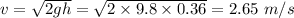

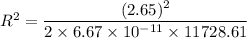
Radius, R = 2118.57 m
Diameter, d = 2R
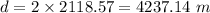
So, the maximum diameter of a spherical asteroid from which you could escape by jumping is 4237.14 meters. Hence, this is the required solution.