Answer: Option C

Explanation:
The number of rabbits in each generation can be modeled using a geometric sequence of the form:
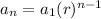
Where
 is the first term of the sequence,
is the first term of the sequence,
 is the ninth term of the series, r is the common ratio
is the ninth term of the series, r is the common ratio
To find the proportion we divide the consecutive terms of the sequence as shown
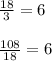
Then the common ratio is:
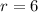
The first term of the series is:
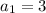
Then the explicit formula is:

The answer is: Option C