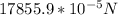Question

What is the magnitude of the force between two parallel wires 43.0 m long and 5.9 cm apart, each carrying 35.0 A in the same direction?

Answer 1

The magnitude of the force between the two wires is
`17855.9*10^(-5) N`

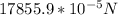
Step-by-step explanation:

If there are two parallel rectilinear conductors through which two electric currents of the same direction I1 and I2 circulate,both conductors will generate a magnetic field on each other, giving rise to a force between them.

To calculate the value of this force, first, according to the law of Biot and Savart, the magnetic field produced by conductor 1 over 2 is obtained, which will be given by the equation:

B1=
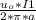`(u_(o)*I1 )/(2*\pi*a )` equation 1

B1: Magnetic field produced by conductor 1

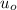`u_(o)` = free space permeability

a= distance between wires

I1= current carrying wire 1

This magnetic field exerts on a segment L of the conductor 2 through which a current of intensity I2 circulates, a force equal to:

F1-2= I2*L*B1 Equation2

We replaced B1 of the equation 1 in the equation 2:

F1-2=
`I2*L*(u_(o)*I1 )/(2*\pi *a)`

F1-2=
`(u_(o)*I1*I2*L )/(2*\pi *a)`

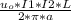
If we calculate the force exerted by conductor 2 on conductor 1 we would arrive at exactly the same value:

F2-1= F1-2

For this problem, the magnitude of the force between the two parallel cables that conduct current in the same direction is:

F1-2=F2-1=F

`u_(o) =4*\pi *10^(-7)`Wb/A.m

I1=I1=35A

L=43M

a =5.9 cm=
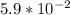`5.9*10^(-2)` m

`F=(4*\pi *10^(-7)*35*35*43 )/(2*\pi *5.9*10^(-2) )`

`F=17855.9*10^(-5) N`

Answer: The magnitude of the force between the two wires is
`17855.9*10^(-5) N`