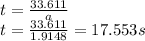Question

A certain aircraft has a liftoff speed of 121 km/h. (a) What minimum constant acceleration does the aircraft require if it is to be airborne after a takeoff run of 295 m? (b) How long does it take the aircraft to become airborne?

Answer 1

A) The minimum constant acceleration is
`1.9148(m)/(s^2)`

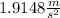
B) The airplane takes 17.553 seconds to become airborne.

Step-by-step explanation:

First, consider the basic equations for the motion with constant acceleration:

`v=v_0+at\\x=x_0+v_0t+(1)/(2)at^2`

Where
`x_0` and
`v_0` are the initial position and velocity respectively; a is the acceleration and t the time.

Let's imagine that the aircraft had become airborne after the 295 m run, and let's model this movement by the last equations. The airplane is considered to be at position zero (
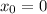`x_0=0` and start from repose (it's start velocity is zero:
`v_0=0`)

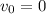Let's convert the velocity to m/s:

`v=121(km)/(h) *(1000m)/(km) *(h)/(3600s) =33.611(m)/(s)`

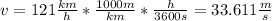
The airplane has a velocity of 33.611 m/s and has run 295 meters when it becomes airborne, so at that time:

`v=v_0+at`

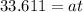`33.611=at` (The initial velocity is zero)

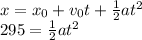`x=x_0+v_0t+(1)/(2)at^2\\295=(1)/(2)at^2` (The initial position is zero)

At this point we have a two-variable-two-equation system; if we could solve it we would know the time and the acceleration.

Let's isolate the time from the first equation and replace it in the second one.

`t=(33.611)/(a)\\t^2=(1129.7)/(a^2) \\295=(1)/(2)at^2\\295=(1)/(2)a*((1129.7)/(a^2) )\\295=(564.85)/(a)`

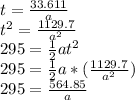
Then, find the acceleration:

`a=(564.85)/(295) =1.9148(m)/(s^2)`

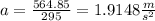
Now, it is possible to find the time by means of any of the initial equations we wrote. Let's take, for example, the first one:

`t=(33.611)/(a)\\t=(33.611)/(1.9148)=17.553s`