Question

(a) What is the ionization energy of a hydrogen atom that is in the n = 6 excited state? (b) For a hydrogen atom, determine the ratio of the ionization energy for the n = 6 excited state to the ionization energy for the ground state.

Answer 1

(a) 0.3778 eV

(b) Ratio = 0.0278

Step-by-step explanation:

The Bohr's formula for the calculation of the energy of the electron in nth orbit is:

`E=\frac {-13.6}{n^2}\ eV`

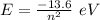
(a) The energy of the electron in n= 6 excited state is:

`E=\frac {-13.6}{6^2}\ eV`

`E=-0.3778\ eV`

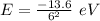
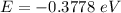
Ionisation energy is the amount of this energy required to remove the electron. Thus, |E| = 0.3778 eV

(b) For first orbit energy is:

`E=\frac {-13.6}{1^2}\ eV`

`E=-13.6\ eV`

`Ratio=\frac {E_6}{E_1}`

`Ratio=\frac {-0.3778}{-13.6}`

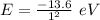
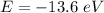
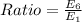
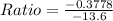
Ratio = 0.0278