Question

a) A 32-pound weight stretches a spring 2 feet. Determine the amplitude and period of motion if the weight is released 1 foot above the equilibrium position with an initial upward velocity of 2 ft/sec. (b) How many complete vibrations will the weight have completed at the end of 4π seconds?

Answer 1

Step-by-step explanation:

Value of spring constant K = weight / extension

=
`(32*32)/(2)`

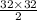
=512 ft s⁻²

Frequency of oscillation of spring mass system

=
`\sqrt{(k)/(m) }`

Putting the values we get

frequency

=
`[tex]\sqrt{(512)/(32) }`[/tex]

= 4 .

Time period = 1 / frequency = .25 s

No of vibrations in 4π second

=
`(4\pi )/(.25)`

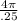
= 50 approx

When the weight is released 1 foot above equilibrium

PE stored = 1/2 K x² = .5 x 512 x 1 = 256 J

KE = 1/2 mv² = .5 x 32 x 4 = 64 J

Total energy = 320 J

Let x be the amplitude upto which spring stretches due to this energy

1/2 k x² = 320 ,

1/2 x 512 x² = 320

x = 1.12 ft approx